斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:0、1、1、2、3、5、8、13、21、34…… ,用函数表示就是:f(n)=f(n-1)+f(n-2),本文就分别用 递归 和 动态规划 算法来求斐波那契数列的第n个值。

一、问题描述
斐波那契数,通常用 f(n) 表示。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和,所以就有以下结果:
f(0)=0
f(1)=1
f(2)=f(0)+f(1)
f(n)=f(n-1)+f(n-2)
斐波那契数列:0、1、1、2、3、5、8、13、21、34……
二、代码演示
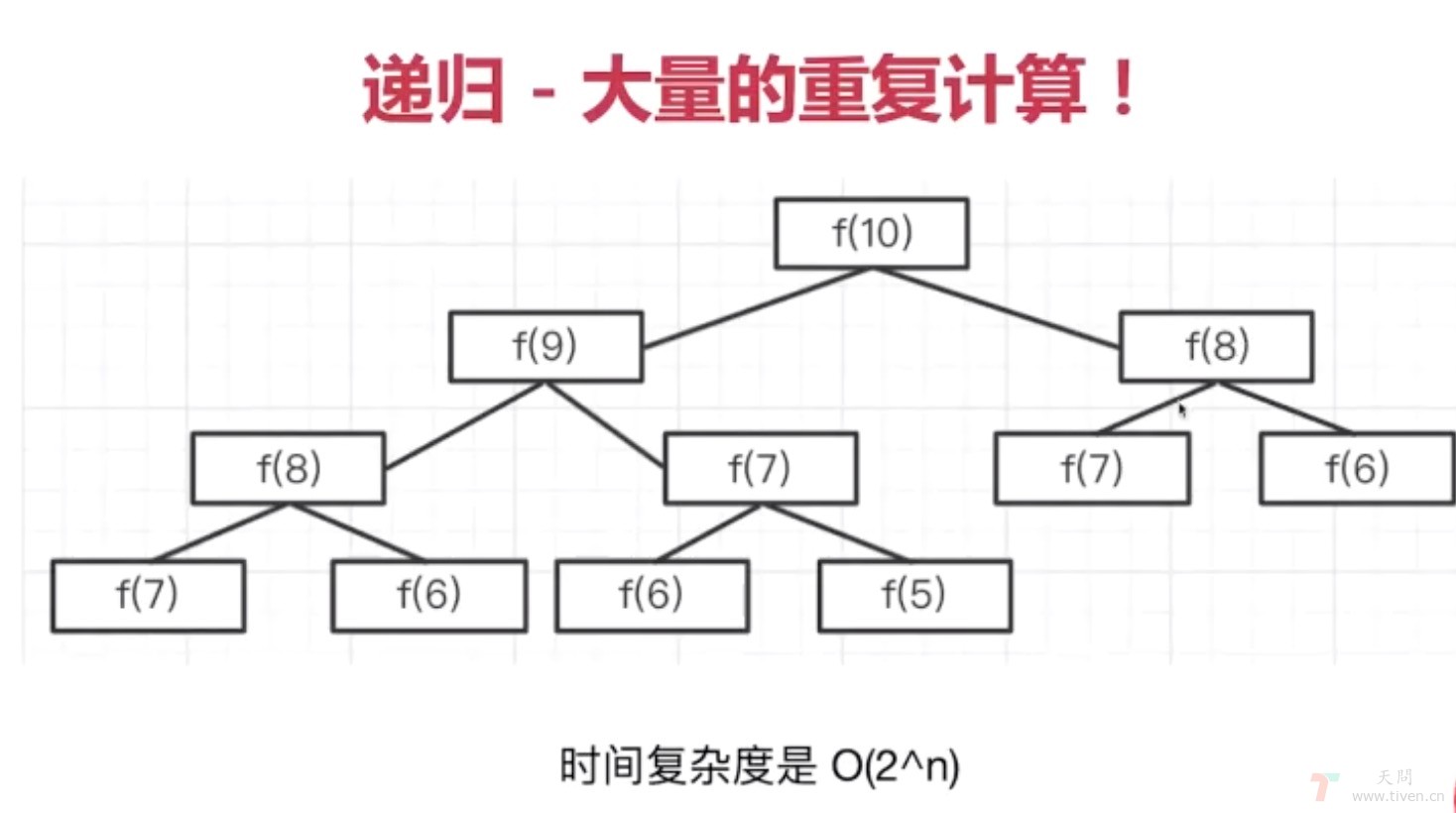
- 暴力递归
function fibonacci1(n: number): number {
if (n<=0) return 0
if (n==1) return 1
return fibonacci1(n-1) + fibonacci1(n-2)
}
- 动态规划
function fibonacci2(n: number): number {
if (n<=0) return 0
if (n==1) return 1
let n1 = 1 // 记录 n-1 的结果
let n2 = 0 // 记录 n-2 的结果
let res = 0
for (let i = 2; i <= n; i++) {
res = n1 + n2
// 记录中间结果
n2 = n1
n1 = res
}
return res
}
- jest 单元测试
describe('斐波那契数列', () => {
it('0 和 1', () => {
expect(fibonacci2(0)).toBe(0)
expect(fibonacci2(1)).toBe(1)
})
it('正常情况', () => {
expect(fibonacci2(2)).toBe(1)
expect(fibonacci2(3)).toBe(2)
expect(fibonacci2(6)).toBe(8)
})
it('n 小于 0', () => {
expect(fibonacci2(-1)).toBe(0)
})
})
三、性能测试
// 暴力递归
console.time('fibonacci1')
fibonacci1(10)
console.timeEnd('fibonacci1')
// 动态规划
console.time('fibonacci2')
fibonacci2(10)
console.timeEnd('fibonacci2')
温馨提示:因为 暴力递归 的算法复杂度为 O(2^n) ,当 n 值较大时算力成本太高,当 n > 40 开始执行明显变慢,当 n > 50 会造成浏览器卡死。
<div> n:<input value="10" id="input" type="number" placeholder="默认n=10"> <br> <button style='padding: 10px 20px; color: #00b1fb;' class='rotate-btn' onclick='run()'>运行</button> <br> <b>斐波那契数列的第 <b style="color: #3BB24D;" class="box-n">0</b> 个值:</b> <span style='color: blueviolet;' class='box-res'>0</span> <br> <b>fibonacci1 run time:</b> <span style='color: red;' class='box1-ms'>0</span> <hr> <b>fibonacci2 run time:</b> <span style='color: red;' class='box2-ms'>0</span> <hr> </div> <script> // 斐波那契数列 递归 function fibonacci1(n) { if (n<=0) return 0 if (n==1) return 1 return fibonacci1(n-1) + fibonacci1(n-2) };
// 斐波那契数列 动态规划 function fibonacci2(n) { if (n<=0) return 0 if (n==1) return 1 let n1 = 1 // 记录 n-1 的结果 let n2 = 0 // 记录 n-2 的结果 let res = 0 for (let i = 2; i <= n; i++) { res = n1 + n2
// 记录中间结果
n2 = n1
n1 = res
}
return res
}
function run() { let n = +input.value.trim() || 10 console.log(n) let s1 = performance.now() let res1 = fibonacci1(n) console.log('fibonacci1', res1) document.querySelector('.box1-ms').innerText = performance.now() - s1 + ' ms'
let s2 = performance.now()
let res2 = fibonacci2(n)
console.log('fibonacci2', res2)
document.querySelector('.box2-ms').innerText = performance.now() - s2 + ' ms'
document.querySelector('.box-n').innerText = n
document.querySelector('.box-res').innerText = res2
} </script>
四、算法复杂度
| 方法 | 时间复杂度 |
|---|---|
| 暴力递归 | O(2^n) |
| 动态规划 | O(n) |
五、拓展
🐸青蛙跳台阶有几种方式?

和斐波那契数列完全一样。
《数据结构与算法》系列
- 什么是算法复杂度
- 堆(heap)、栈(stack)、队列(queue)
- 把一个数组旋转k步
- 判断字符串是否括号匹配
- 数组、栈、链表、队列结构与对比
- 用两个栈实现一个队列
- 反转单向链表
- 用链表实现队列
- 二分查找
- 查找两数之和
- 求斐波那契数列的第n个值
欢迎访问:天问博客