【数据结构与算法】(12)：二叉树

二叉树 是一种典型的树树状结构。从名称就可得知，二叉树是每个节点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。本文就介绍一下二叉树的遍历，拓展应用，以及堆与二叉树的关系。

一、二叉树特点

1. 是一个树状结构
2. 每个节点，最多只能有 2 个子节点
3. 树节点的数据结构 {value, left?, right?}

二、二叉树遍历

• 二叉树 interface

export interface ITreeNode {
  value: number
  left: ITreeNode | null
  right: ITreeNode | null
}

• 二叉树节点示例

export const tree: ITreeNode = {
  value: 5,
  left: {
    value: 3,
    left: {
      value: 2,
      left: null,
      right: null
    },
    right: {
      value: 4,
      left: null,
      right: null
    }
  },
  right: {
    value: 7,
    left: {
      value: 6,
      left: null,
      right: null
    },
    right: {
      value: 8,
      left: null,
      right: null
    }
  },
}

1）二叉树 前序遍历

1. 递归实现

// 二叉树 前序遍历
export function preOrderTraverse(node: ITreeNode | null, arr: number[]): number[] | null {
  if (node===null) return arr
  arr.push(node.value);
  preOrderTraverse(node.left, arr);
  preOrderTraverse(node.right, arr);
  return arr;
}

2. 栈实现

export function preOrderTraverse2(node: ITreeNode): number[] | null{
  const res: number[] = []
  const stack:ITreeNode[] = []
  stack.push(node)
  while (stack.length) {
    let current = stack.pop()
    if (!current) break
    res.push(current.value)
    if (current.right) stack.push(current.right)
    if (current.left) stack.push(current.left)
  }

  return res
}

2）二叉树 中序遍历

1. 递归实现

// 二叉树 中序遍历
export function inOrderTraverse(node: ITreeNode | null, arr: number[]): number[] | null {
  if (node===null) return arr
  inOrderTraverse(node.left, arr);
  arr.push(node.value);
  inOrderTraverse(node.right, arr);
  return arr;
}

2. 栈实现

export function inOrderTraverse2(node: ITreeNode | null): number[] | null{
  const res: number[] = []
  const stack:ITreeNode[] = []
  let current: ITreeNode | null = node
  while (current!==null || stack.length) {
    while (current!==null) {
      stack.push(current)
      current = current.left
    }
    current = stack.pop() || null
    res.push(current!.value)
    current = current!.right
  }

  return res
}

3）二叉树 后序遍历

1. 递归实现

// 二叉树 后序遍历
export function postOrderTraverse(node: ITreeNode | null, arr: number[]): number[] | null {
  if (node===null) return arr
  postOrderTraverse(node.left, arr);
  postOrderTraverse(node.right, arr);
  arr.push(node.value);
  return arr;
}

2. 栈实现

export function postOrderTraverse2(node: ITreeNode): number[] | null{
  const res: number[] = []
  const stack:ITreeNode[] = []
  stack.push(node)
  while (stack.length) {
    let current = stack.pop()
    if (!current) break
    if (current.left) stack.push(current.left)
    if (current.right) stack.push(current.right)
    res.unshift(current.value)
  }

  return res
}

4）结果输出

测试：

// 二叉树 前序遍历
console.log('preOrderTraverse')
console.log(preOrderTraverse(tree, []))

// 二叉树 中序遍历
console.log('inOrderTraverse')
console.log(inOrderTraverse(tree, []))

// 二叉树 后序遍历
console.log('postOrderTraverse')
console.log(postOrderTraverse(tree, []))

输出：

preOrderTraverse
[5, 3, 2, 4, 7, 6, 8]

inOrderTraverse
[2, 3, 4, 5, 6, 7, 8]

postOrderTraverse
[2, 4, 3, 6, 8, 7, 5]

三、二叉搜索树 BST

1）二叉搜索树 BST (Binary Search Tree) 特点

1. left (包括其后代) value <= root value
2. right (包括其后代) value >= root value
3. 可使用 二分法 进行快速查找

2）数组 vs 链表 vs 二叉搜索树

数组： 查找快 O(1)，增删慢 O(n) 链表： 查找慢 O(n)，增删快 O(1) 二叉搜索树 BST： 查找快 O(logn)，增删快

3）求一个二叉搜索树的第 K 小值

如图：

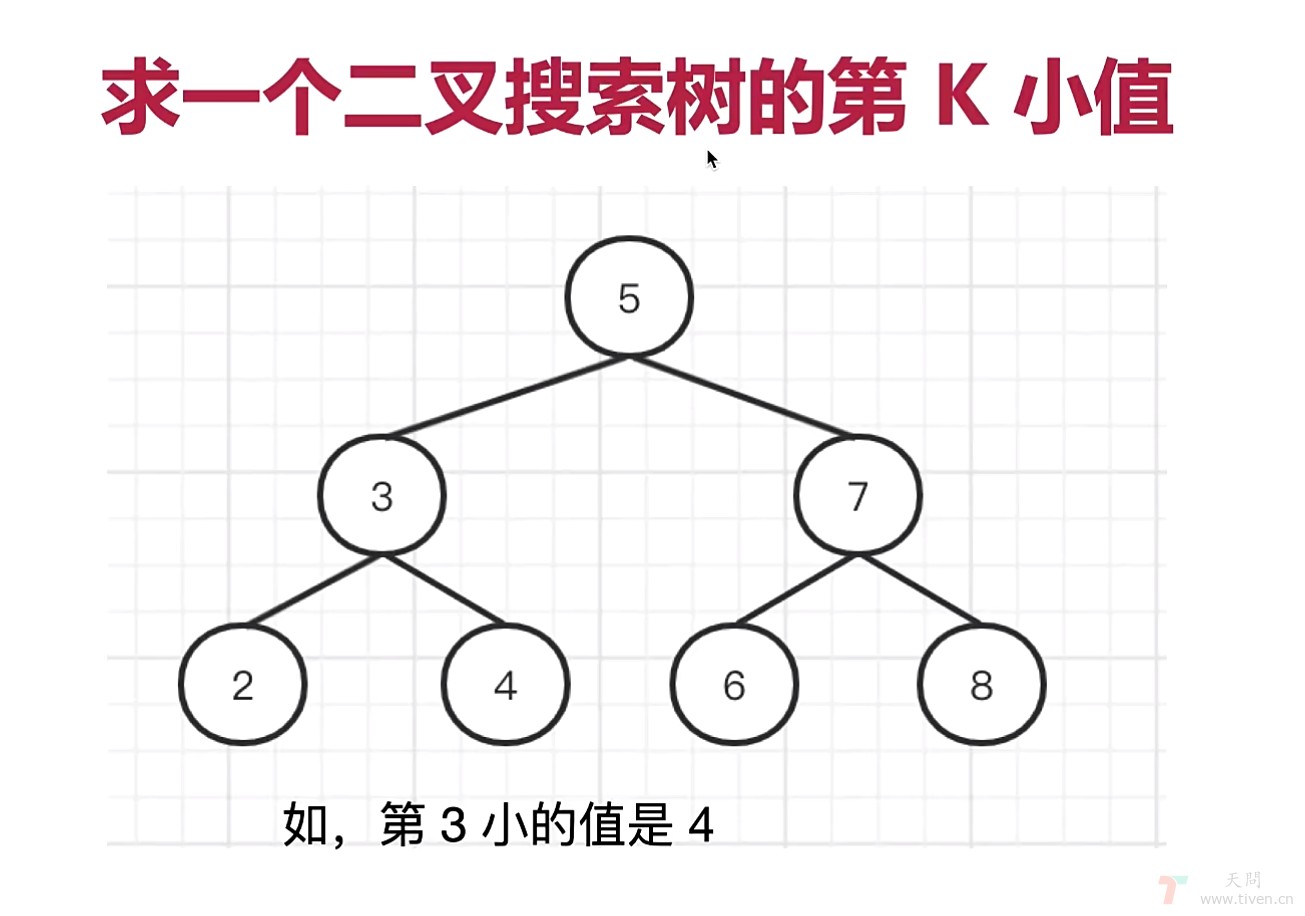
思路：二叉搜索树在中序遍历后，可返回一个有序递增的数组，所以求一个二叉搜索树的第 K 小值就变得很简单，代码如下：

export function getKthValue(node: ITreeNode, k: number) :number | null {
  let res = inOrderTraverse(node, []) || []
  return res[k - 1] || null
}

四、红黑树

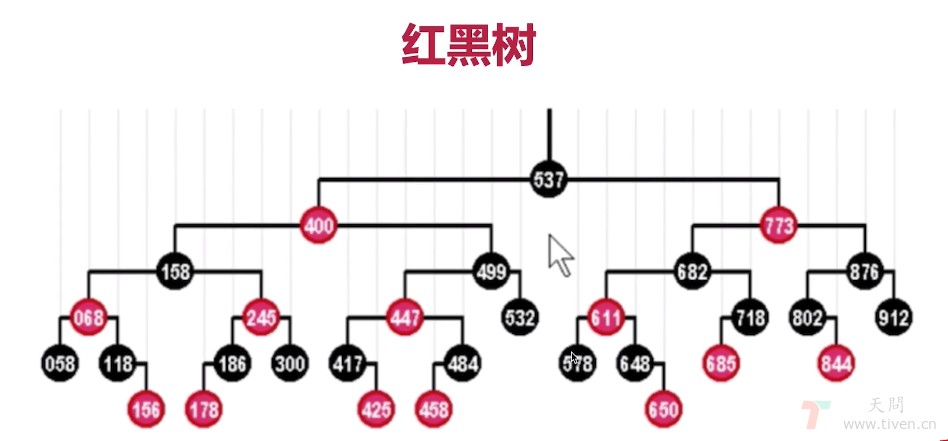
特点：

1. 一种自平衡二叉树
2. 分为 红/黑 两种颜色，通过颜色转换来维持树的平衡
3. 相对于普通平衡二叉树，它维持平衡的效率更高

五、B 树

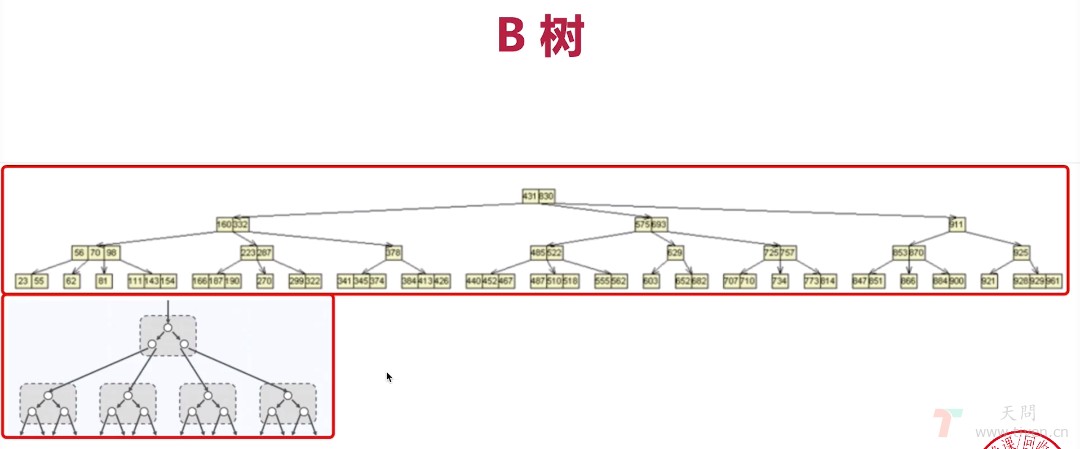
六、堆 Heap

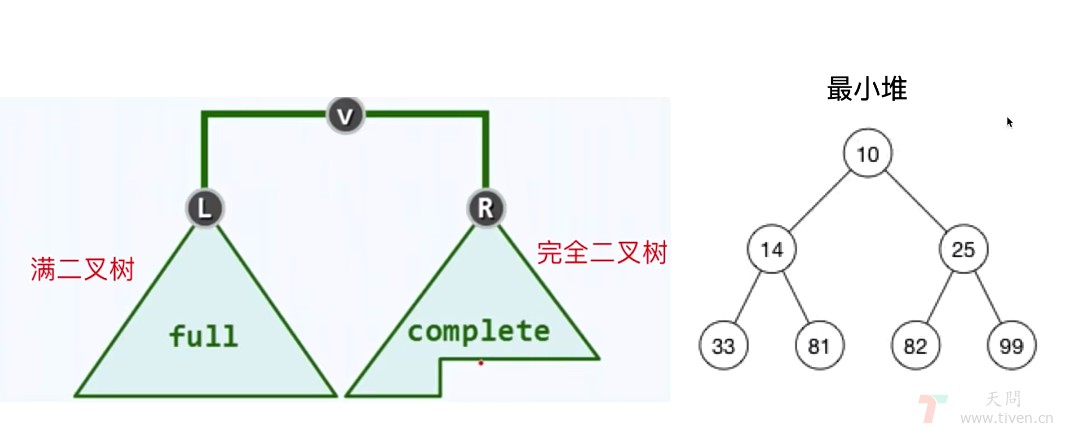
特点：

1. 堆（Heap） 是完全二叉树，比 BST 结构灵活
2. 最小堆：父节点 <= 子节点
3. 最大堆：父节点 >= 子节点

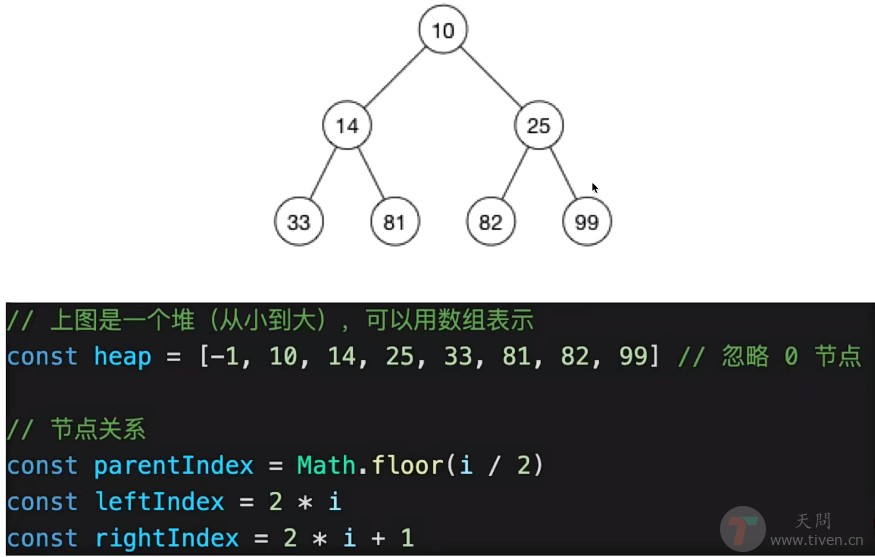
结构：

• 堆，逻辑结构 是一颗二叉树，查找快
• 物理结构 是一个数组，连续存储，节省空间
• 堆栈模型（基础类型和引用类型）

堆 vs BST

• 堆查询比 BST 慢
• 堆删除比 BST 快，维持平衡更快
• 整体时间复杂度都是 O(logn) 级别，即树的高度（层级）

欢迎访问：天问博客